검색결과 리스트
글
SVM 알고리즘
서포트 벡터 머신(support vector machine, SVM)은 분류 과제에 사용할 수 있는 강력한 머신러닝 지도학습 모델이다.
그래서 분류되지 않은 새로운 점이 나타나면 경계의 어느 쪽에 속하는지 확인해서 분류 과제를 수행할 수 있게 된다.
결국 이 결정 경계라는 걸 어떻게 정의하고 계산하는지 이해하는 게 중요하다는 뜻이다.
일단 예시를 보자.
만약 데이터에 2개 속성(feature)만 있다면 결정 경계는 이렇게 간단한 선 형태가 될 거다.

그러나 속성이 3개로 늘어난다면 이렇게 3차원으로 그려야 한다.

그리고 이 때의 결정 경계는 ‘선’이 아닌 ‘평면’이 된다.
우리가 이렇게 시각적으로 인지할 수 있는 범위는 딱 3차원까지다. 차원, 즉 속성의 개수가 늘어날수록 당연히 복잡해질 거다. 결정 경계도 단순한 평면이 아닌 고차원이 될 텐데 이를 “초평면(hyperplane)”이라고 부른다. (어렵게 생각할 필요는 없다. 일단 용어만 알고 넘어가자.)
최적의 결정 경계(Decision Boundary)
결정 경계는 무수히 많이 그을 수 있을 거다. 어떤 경계가 좋은 경계일까?
일단 아래 그림들을 보자.

어떤 그래프가 제일 위태로워 보이는가?
C를 보면 선이 파란색 부류와 너무 가까워서 아슬아슬해보인다.
그렇다면 어떤 결정 경계가 가장 적절해보이는가?
당연히 F다. 두 클래스(분류) 사이에서 거리가 가장 멀기 때문이다.
이제 결정 경계는 데이터 군으로부터 최대한 멀리 떨어지는 게 좋다는 걸 알았다. 실제로 서포트 벡터 머신(Support Vector Machine)이라는 이름에서 Support Vectors는 결정 경계와 가까이 있는 데이터 포인트들을 의미한다. 이 데이터들이 경계를 정의하는 결정적인 역할을 하는 셈이다.
이어서 마진(Margin)이라는 용어에 대해 알아보자.
마진(Margin)
마진(Margin)은 결정 경계와 서포트 벡터 사이의 거리를 의미한다.
아래 그림을 보면 바로 이해된다.
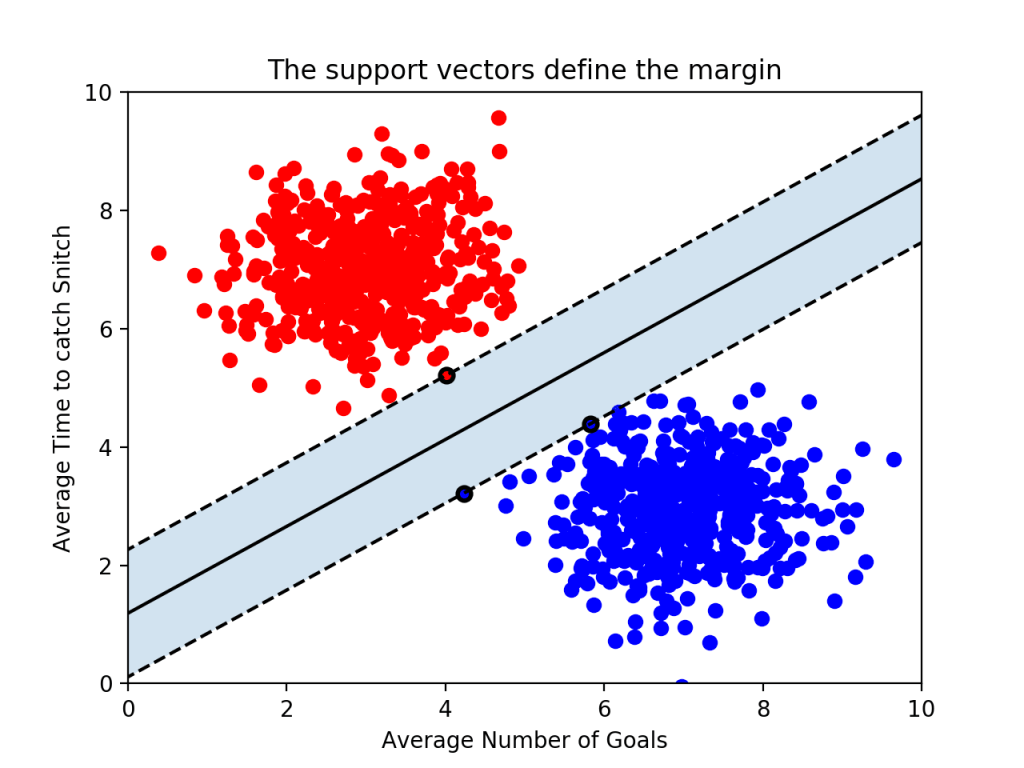
가운데 실선이 하나 그어져있는데, 이게 바로 ‘결정 경계’가 되겠다. 그리고 그 실선으로부터 검은 테두리가 있는 빨간점 1개, 파란점 2개까지 영역을 두고 점선을 그어놓았다. 점선으로부터 결정 경계까지의 거리가 바로 ‘마진(margin)’이다.
여기서 일단 결론을 하나 얻을 수 있다. 최적의 결정 경계는 마진을 최대화한다.
그리고 위 그림에서는 x축과 y축 2개의 속성을 가진 데이터로 결정 경계를 그었는데, 총 3개의 데이터 포인트(서포트 벡터)가 필요했다. 즉, n개의 속성을 가진 데이터에는 최소 n+1개의 서포트 벡터가 존재한다는 걸 알 수 있다.
이번엔 SVM 알고리즘의 장점을 하나 알 수 있다.
대부분의 머신러닝 지도 학습 알고리즘은 학습 데이터 모두를 사용하여 모델을 학습한다. 그런데 SVM에서는 결정 경계를 정의하는 게 결국 서포트 벡터이기 때문에 데이터 포인트 중에서 서포트 벡터만 잘 골라내면 나머지 쓸 데 없는 수많은 데이터 포인트들을 무시할 수 있다. 그래서 매우 빠르다.
이상치(Outlier)를 얼마나 허용할 것인가
SVM은 데이터 포인트들을 올바르게 분리하면서 마진의 크기를 최대화해야 하는데, 결국 이상치(outlier)를 잘 다루는 게 중요하다.
아래 그림을 보자. 선을 살펴보기에 앞서 왼쪽에 혼자 튀어 있는 파란 점과, 오른쪽에 혼자 튀어 있는 빨간 점이 있다는 걸 봐두자. 누가 봐도 아웃라이어다.
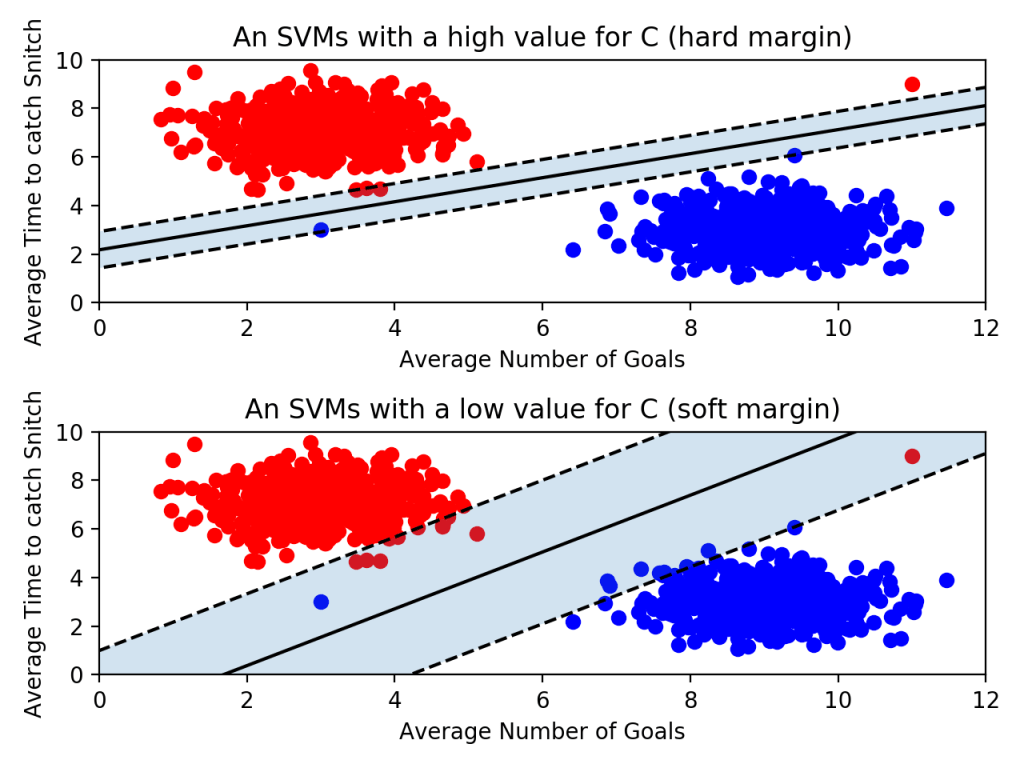
이제 위 아래 그림을 좀 더 자세히 비교해보자.
- 위의 그림은 아웃라이어를 허용하지 않고 기준을 까다롭게 세운 모양이다. 이걸 하드 마진(hard margin)이라고 부른다. 그리고 서포트 벡터와 결정 경계 사이의 거리가 매우 좁다. 즉, 마진이 매우 작아진다. 이렇게 개별적인 학습 데이터들을 다 놓치지 않으려고 아웃라이어를 허용하지 않는 기준으로 결정 경계를 정해버리면 오버피팅(overfitting) 문제가 발생할 수 있다.
- 아래 그림은 아웃라이어들이 마진 안에 어느정도 포함되도록 너그럽게 기준을 잡았다. 이걸 소프트 마진(soft margin)이라고 부른다. 이렇게 너그럽게 잡아 놓으니 서포트 벡터와 결정 경계 사이의 거리가 멀어졌다. 즉, 마진이 커진다. 대신 너무 대충대충 학습하는 꼴이라 언더피팅(underfitting) 문제가 발생할 수 있다.
커널(Kernel)
지금까지는 선형으로 결정 경계를 그을 수 있는 형태의 데이터 세트를 예시로 들었다. 그런데 만약 SVM이 선형으로 분리 할 수 없는 데이터 세트가 있다면 어떻게 해야 할까?
극단적인 예를 들어… 이런 데이터가 있다고 해보자.

빨간색 점을 파란색 점과 분리하는 직선을 그릴 수가 없다..!
위에서 다룬 내용을 가볍게 요약하면 아래와 같다.
- SVM은 분류에 사용되는 지도학습 머신러닝 모델이다.
- SVM은 서포트 벡터(support vectors)를 사용해서 결정 경계(Decision Boundary)를 정의하고, 분류되지 않은 점을 해당 결정 경계와 비교해서 분류한다.
- 서포트 벡터(support vectors)는 결정 경계에 가장 가까운 각 클래스의 점들이다.
- 서포트 벡터와 결정 경계 사이의 거리를 마진(margin)이라고 한다.
- SVM은 허용 가능한 오류 범위 내에서 가능한 최대 마진을 만들려고 한다.
- 파라미터 C는 허용되는 오류 양을 조절한다. C 값이 클수록 오류를 덜 허용하며 이를 하드 마진(hard margin)이라 부른다. 반대로 C 값이 작을수록 오류를 더 많이 허용해서 소프트 마진(soft margin)을 만든다.
- SVM에서는 선형으로 분리할 수 없는 점들을 분류하기 위해 커널(kernel)을 사용한다.
- 커널(kernel)은 원래 가지고 있는 데이터를 더 높은 차원의 데이터로 변환한다. 2차원의 점으로 나타낼 수 있는 데이터를 다항식(polynomial) 커널은 3차원으로, RBF 커널은 점을 무한한 차원으로 변환한다.
SVM은 다음과 같은 현실 세계의 문제들을 해결하는데 사용된다:
- SVM은 텍스트와 하이퍼텍스트를 분류하는데 있어서, 학습 데이터를 상당히 줄일 수 있게 해준다.
- 이미지를 분류하는 작업에서 SVM을 사용할 수 있다. SVM이 기존의 쿼리 개량 구조보다 상당히 높은 검색 정확도를 보인 것에 대한 실험 결과가 있다.
- SVM은 분류된 화합물에서 단백질을 90%까지 구분하는 의학 분야에 유용하게 사용된다.
- SVM을 통해서 손글씨의 특징을 인지할 수 있다.
*코랩 테스트
https://colab.research.google.com/drive/1q3GGhRpjJAoSLTalkhIS-i5cxW2p9pus#scrollTo=Vr_crhIkDcZW
'Tensorflow 정리' 카테고리의 다른 글
| base64 서명 데이터 학습 (0) | 2021.07.20 |
|---|---|
| 머신러닝 모델 배포 방법 (0) | 2021.06.29 |
| TensorFlow 연습 (0) | 2021.05.19 |
